数据结构：树(tree)

1. 树(tree)

1.1 概念

1.1.1 树的定义

树（Tree）是 n(n >= 0) 个结点的有限集。
n = 0 时称为空树。
在任意一颗非空树中：
- 有且仅有一个特定的称为根（root）的结点
- 当 n > 1 时，其余结点可分为 m(m>0) 个互不相交的有限集 T1 、T2 ... Tn ，其中每一个集合本身有事一棵树，并且称为根的子树（SubTree)

1.1.2 树的分类

树的结点包含一个数据元素及若干指向其子树的分支；
结点拥有的子树数称为结点的度（Degree）；
度为0的结点称为叶结点（Leaf）或终端结点；
度不为0的结点称为非终端结点或分支结点；
除根结点之外，分支结点也称为内部结点。
树的度是树内各结点的度的最大值；

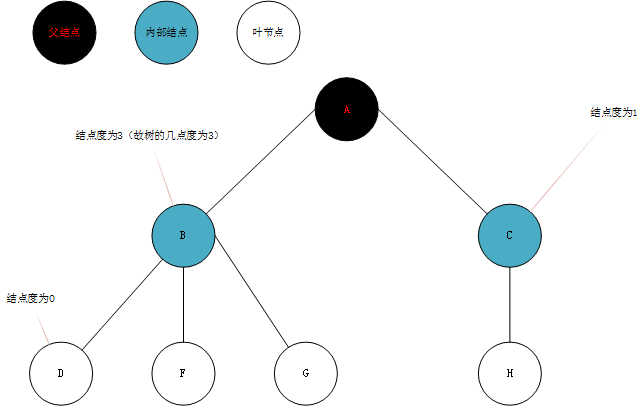
5.tree-category

1.1.3 结点间关系

结点的子树的根称为该结点的孩子**（Child）**
该结点称为孩子的双亲**（Parent）**
同一个双亲的孩子之间互称兄弟**（Sibling）**。
结点的祖先是从根到该结点所经分支上的所有结点。
以某结点为根的子树中的任一结点都称为该结点的子孙。

1.1.4 其他概念

结点的层次**（Level）**
- 根为第一层，根的孩子为第二层，依次类推。
- 树中结点的最大层次称为树的深度（Depth）或高度
如果将树中结点的各子树看成从左至右是有次序的，不能互换的，则称该树为有序树，否则称为无序树。
**森林（Forest）**是m（m>0）棵互不相交的树的集合。对树中每个结点而言，其子树的集合即为森林。

1.2 树的抽象数据类型

c
ADT树(tree)
	Data树是由一个根结点和若干棵子树构成。树中结点具有相同数据类型及层次关系。
Operation 
	InitTree(*T):构造空树T。
	DestroyTree(*T):销毁树T。
	CreateTree(*T,definition):按definition中给出树的定义来构造树。
	ClearTree(*T):若树T存在,则将树T清为空树。
	TreeEmpty(T):若T为空树,返回true,否则返回false。
	Treepepth(T):返回T的深度。
	Root(T):返回T的根结点。
	Value(T,cur_e):cur_e是树T中一个结点,返回此结点的值。
	Assign(T,cur_e,value):给树T的结点cur_e赋值为value。
	Parent(T,cur_e):若cur_e是树T的非根结点,则返回它的双亲,否则返回空。
	Leftchild(T,cur_e):若cur_e是树T的非叶结点,则返回它的最左孩子,否则返回空。
	RightSibling(T,cur_e):若cur_e有右兄弟,则返回它的右兄弟,否则返回空。
	InsertChild(*T,*p,i,c):其中p指向树T的某个结点,i为所指结点p的度加上1,非空树c与T不相交,操作结果为插入c为树T中p指结点的第棵子树。
	Deletechild(*T,*p,i):其中p指向树T的某个结点,i为所指结点p的度,操作结果为删除T中p所指结点的第i棵子树。
endADT

1.3 树的存储结构

1.3.1 双亲表示法

在每个结点中，附设一个指示器指示其双亲结点到链表中的位置

这种设置，我们可以很快找到结点的根节点，但是想要找到子结点，只能通过遍历整个结构，所以为了解决该问题，可以为其结点增加长子域，右兄弟域等等

1.3.2 孩子表示法

1.3.2.1多重链表表示法

每个结点设置多个指针域，其中每个指针指向一颗子树有的根节点，我们吧这种方法叫做多重链表表示法

由于树的每个结点的度是不同的，所以有以下两种方案来解决

1.3.2.1.1 方案一（固定大小的指针域）

用树的度作为作为指针域的大小去构建结点（树的度：树内各结点的度的最大值）

以这种方案去构建，当树内各个结点的度相差比较远的时候，会造成空间浪费，相反，当树内各个结点的度相差比较小的时候，则该存储结构有更高的优势（减少运算）

1.3.2.1.2 方案二（按需分配的指针域）

每个结点指针域的个数等于该结点的度，用一个位置来存储结点指针域的个数

这种方法克服了浪费空间的缺点，对空间利用率提高了，但是由于各个结点的链表结构式不同的，加上要维护结点的度的数值，运算上会带来时间上的损耗

1.3.2.2 孩子表示法

把每个结点的孩子结点排列起来，以单链表作存储结构，则 n 个结点有 n 个孩子链表，如果叶子结点则此单链表为空。然后 n 个头指针又组成一个线性表，采用顺序存储结构，存放进一个一维数组中

1.3.3 双亲孩子表示法

孩子表示法对于查找孩子的双亲比较麻烦，于是结合孩子标识法和双亲表示法，构建一个双亲孩子表示法

在孩子表示法中增加存放双亲结点指针的指针域

2. 二叉树（Binary Tree)

二叉树是 n ( n >= 0 ) 个结点的有限集合，改集合或者为空集（称为空二叉树），或者由一个根结点和两颗互不想交的、分别称为根结点的左子树和右子树的二叉树组成

2.1 二叉树的特点

特点：
- 每个结点最多有两棵子树，所以二又树中不存在度大于2的结点。注意不是只有两棵子树，而是最多有。没有子树或者有一棵子树都是可以的。
- 左子树和右子树是有顺序的，次序不能任意颠倒。就像人是双手、双脚，但显然左手、左脚和右手、右脚是不一样的，右手戴左手套、右脚穿左鞋都会极其别扭和难受。
- 即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。
形态：
- 空二叉树
- 只有根结点
- 只有一个左子树
- 只有一个右子树
- 既有左子树，又有右子树

2.2 特殊二叉树

2.2.1 斜树

所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。

2.2.2 满二叉树

在一颗二叉树中，如果所有分支结点都存在左子树和右子树，并且所以叶子都在同一层中

2.2.3 完全二叉树

对一棵具有 n 个结点的二叉树按层序编号，如果编号为 i（1 < i < n）的结点与同样深度的满二又树中编号为i的结点在二又树中位置完全相同，则这棵二叉树称为完全二叉树

叶子结点只能出现在最下两层。
最下层的叶子一定集中在左部连续位置。
倒数二层，若有叶子结点，一定都在右部连续位置。
如果结点度为1，则该结点只有左孩子，即不存在只有右子树的情况。
同样结点数的二又树，完全二叉树的深度最小。

2.3 二叉树的性质

性质1:

在二叉树的 i 层上最多结点数 = 2^{i-1}(i \geq 1)

性质2：

深度为k的二叉树至多有 2^K-1(K \geq 1) 个结点

性质3：

对任何一棵二又树 T，如果其终端结点数(叶子数)为 n_0，度为 2 的结点数为 n_2，则 n_0 = n_2 + 1

性质4：

具有 n 个结点的完全二叉树的深度为 [log_2n] + 1 ([x] 表示不大于 x 的最大值)

性质5：

如果对一颗有 n 个结点的完全二叉树（其深度为[log_2n]+1)的结点按层序编号\\ （从第1层到低[log2n]+1层，每层从左到右），对任一结点 i（1 \leq i \leq n)有：\\ 1.如果 i=1,则结点 i 是二叉树的根，五双亲；如果 i > 1,则其双亲是结点[i/2] \\ 2.如果 2i>n ,则结点 i 无左孩子（结点i为叶子结点）；否则其左孩子是结点 2i； \\ 3.如果 2i+1>n,则结点i无右孩子；否则其右孩子是结点2i+12 \\

2.4 二叉树的存储结构

2.4.1 顺序存储结构

2.4.2 链表存储结构

2.5 二叉树的遍历(traversing binary tree)

二叉树的遍历是指从根结点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点被访问一次且仅被访问一次

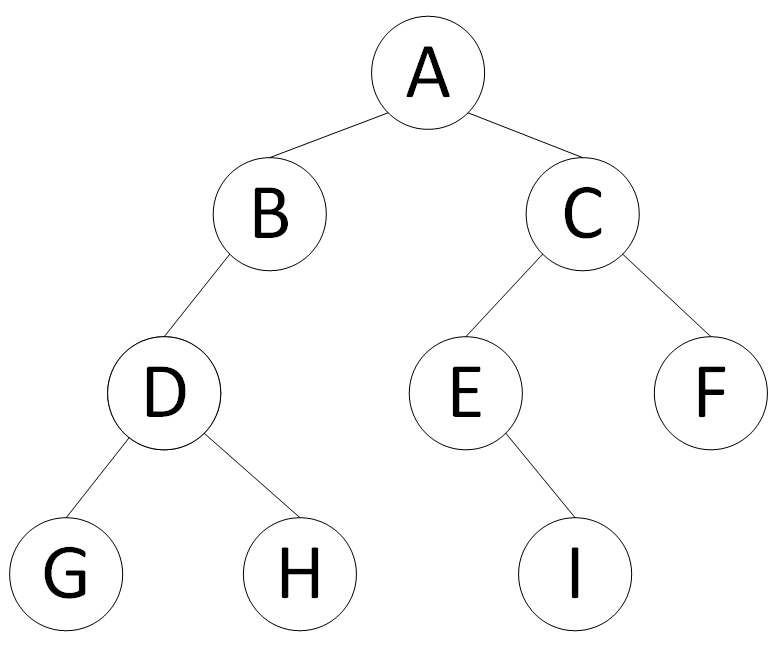
5.tree-a-tree

2.5.1 前序遍历

规则是若二叉树为空，则空操作返回，否则先返回根结点，然后前序遍历左子树，再遍历右子树。上图的前序遍历顺序为：ABDGHCEIF

2.5.2 中序遍历

规则是若二叉树为空，则空操作返回，否则从根结点开始（注意并不是先访问根节点），中序遍历根节点的左子树，然后访问根结点，最后中序遍历右子树。上图的中序遍历顺序为：GDHBAEICF

2.5.3 后序遍历

规则是若二叉树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历左右子树，最后访问根节点。上图的后续遍历顺序为：GHDBIEFCA

2.5.4 层序遍历

规则是若二叉树为空，则空操作返回，否则从树的第一层，也就是根节点开始访问，冲上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问。上图的层序遍历顺序为：ABCDEFGHI

2.5.5 推导树的结构

已知前序遍历序列和中序遍历序列，可以唯一确定一棵二叉树。
已知后序遍历序列和中序遍历序列，可以唯一确定一棵二叉树。

2.6 二叉树的建立

与二叉树的遍历一致

2.7 线索二叉树

这种指向前驱和后继的指针称为线索，加上线索的二叉链表称为线索链表，相应的二又树就称为线索二又树（Threaded Binary Tree）。

使为空的左孩子指针指向该结点的前驱，为空的右孩子指针指向该结点的后继；并设置标记，ltag 和 rtag ，为 0时指向孩子，为 1 时指向前驱、后继。（主要是为了充分利用空指针域）

3. 树、森林、二叉树的转换

3.1 树转二叉树

步骤：

加线。在所有兄弟结点之间加一条连线。
去线。对树中每个结点，只保留它与第一个孩子结点的连线，删除它与其他孩子结点之间的连线。
层次调整。以树的根结点为轴心，将整棵树顺时针旋转一定的角度，使之结构层次分明。注意第一个孩子是二叉树结点的左孩子，兄弟转换过来的孩子是结点的右孩子。

树：

graph TB;
    1((A)) --- 2((B))
    1((A)) --- 3((C))
    1((A)) --- 4((D))
    2((B)) --- 5((E))
    2((B)) --- 6((F))
    2((B)) --- 7((G))
    3((C)) --- 8((H))
    4((D)) --- 9((I))
    4((D)) --- 10((J))

变化过程-连线：

graph TB;
    1((A)) --- 2((B))
    1((A)) --- 3((C))
    1((A)) --- 4((D))
    2((B)) --- 5((E))
    2((B)) --- 6((F))
    2((B)) --- 7((G))
    3((C)) --- 8((H))
    4((D)) --- 9((I))
    4((D)) --- 10((J))
    
    2 -.- 3
    3 -.- 4
    
    5 -.- 6
    6 -.- 7
    
    9 -.- 10

变化过程-删除连线：

graph TB;
    1((A)) --- 2((B))
    2((B)) --- 5((E))
    3((C)) --- 8((H))
    4((D)) --- 9((I))
    
    2 -.- 3
    3 -.- 4
    
    5 -.- 6((F))
    6 -.- 7((G))
    
    9((I)) -.- 10((J))

3.2 森林转二叉树

步骤：

把每个树转换为二又树。
第一棵二叉树不动，从第二棵二叉树开始，依次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子，用线连接起来。当所有的二又树连接起来后就得到了由森林转换来的二叉树。

3.3 二叉树转树

步骤：

加线。若某结点的左孩子结点存在，则将这个左孩子的右孩子结点、右孩子的右孩子结点、右孩子的右孩子的右孩子结点……哈，反正就是左孩子的 n 个右孩子结点都作为此结点的孩子。将该结点与这些右孩子结点用线连接起来。
去线。删除原二叉树中所有结点与其右孩子结点的连线。
层次调整。使之结构层次分明。

3.4 二叉树转森林

判断一棵二又树能够转换成一棵树还是森林，标准很简单，那就是只要看这棵二又树的根结点有没有右孩子，有就是森林，没有就是一棵树。那么如果是转换成森林，步骤如下：

从根结点开始，若右孩子存在，则把与右孩子结点的连线删除，再查看分离后的二叉树，若右孩子存在，则连线删除……，直到所有右孩子连线都删除为止，得到分离的二叉树。
再将每棵分离后的二又树转换为树即可。

目录

1. 树(tree)

1.1 概念

1.1.1 树的定义

1.1.2 树的分类

1.1.3 结点间关系

1.1.4 其他概念

1.2 树的抽象数据类型

1.3 树的存储结构

1.3.1 双亲表示法

1.3.2 孩子表示法

1.3.2.1多重链表表示法

1.3.2.1.1 方案一（固定大小的指针域）

1.3.2.1.2 方案二（按需分配的指针域）

1.3.2.2 孩子表示法

1.3.3 双亲孩子表示法

2. 二叉树（Binary Tree)

2.1 二叉树的特点

2.2 特殊二叉树

2.2.1 斜树

2.2.2 满二叉树

2.2.3 完全二叉树

2.3 二叉树的性质

2.4 二叉树的存储结构

2.4.1 顺序存储结构

2.4.2 链表存储结构

2.5 二叉树的遍历(traversing binary tree)

2.5.1 前序遍历

2.5.2 中序遍历

2.5.3 后序遍历

2.5.4 层序遍历

2.5.5 推导树的结构

2.6 二叉树的建立

2.7 线索二叉树

3. 树、森林、二叉树的转换

3.1 树转二叉树

3.2 森林转二叉树

3.3 二叉树转树

3.4 二叉树转森林